@ 시간 복잡도란?
- 입력을 나타내는 문자열 길이의 함수로서 작동하는 알고리즘을 취해 시간을 정량화하는 것. 알고리즘의 시간복잡도는 주로 Big-O 표기법을 사용하여 나타내고 있다.
- 알고리즘의 logic을 코드로 구현할 때, Time Complexity를 고려한다는 것은 무엇일까?
- 입력값의 변화에 따라 연산을 실행할 떄, 연산 횟수에 비해 시간이 얼마나 걸리는 가를 의미한다.
- 따라서 효율적인 알고리즘을 구현한다는 것은 입력값에 따른 시간의 비율을 최소화한 알고리즘을 구성했다라 생각하면 된다.
@ Big-O 표기법
==> 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마나 걸리는가
- Big-O 표기법은 상한 점근, 즉 최악의 경우를 고려하는 표기법이다. 최악의 경우를 고려하므로, 프로그램이 실행되는 최악의 시간까지를 고려할 수 있다.
- 다르게 생각해 최선(Big-Ω)을 고려한다 생각하면 최선의 경우 짧은 시간이 걸렸다 해도 실제로 많은 시간이 투자됐다면 어디서 문제점이 생겼는지 파악하는 게 쉽지 않다. 따라서 logic의 거의 다 봐야하므로 문제를 파악하는 데 많은 시간이 필요하다.
- 평균(Big-θ)을 고려할 경우 최악인 경우가 발생한다면 최선일 때 고려한 것과 같은 고민을 하게 된다.
- 위에 두개의 상황은 극단적 상황을 예시로 본 것이다. 그러나 최악의 경우를 대비하는게 시간을 아끼는 길이지 않을까 생각된다.
@ Big-O 표기법의 종류
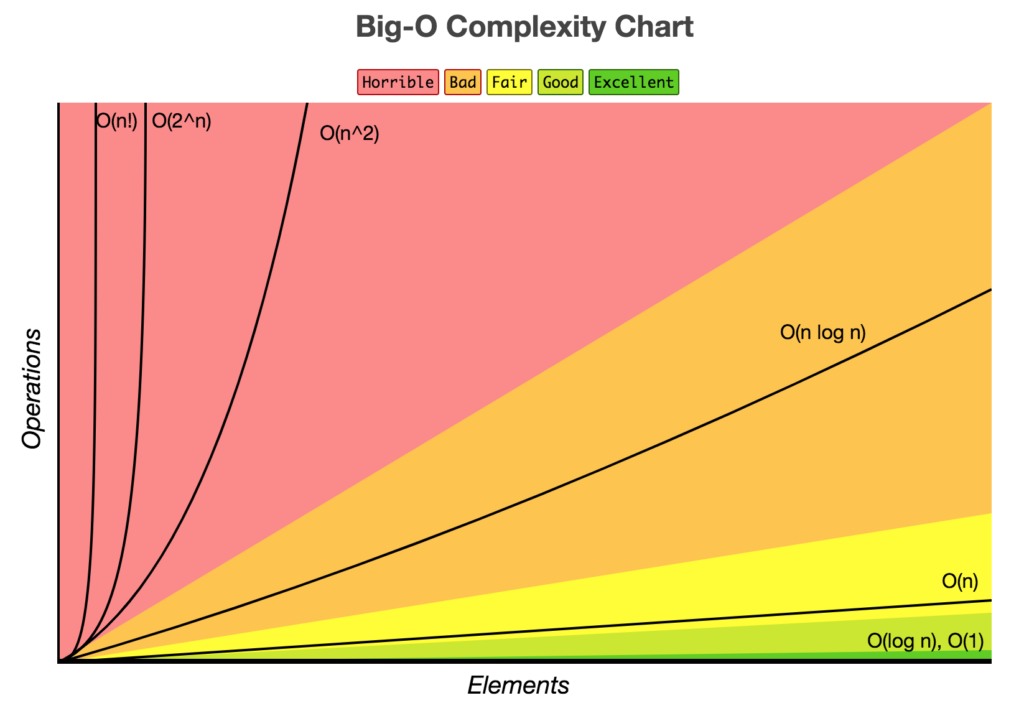
1. O(1): 문제를 해결하는데 오직 한 단계만 처리함. (constant complexity)
function ex(arr) {
console.log(arr[0]);
}
2. O(n): 문제를 해결하기 위한 단계의 수와 입력 값이 n이 같은 비율을 가진다. (linear complexity)
function ex(n) {
for (let i = 0; i < n; i++) {
console.log(i);
}
}
3. O(log n): 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어든다. (logarithmic complexity)
function exampleLogarithmic(n) {
for (let i = 2; i <= n; i*2) {
console.log(i);
}
}
4. O(n log n): 문제를 해결하기 위한 단계의 수가 N*(log2N) 번만큼 수행시간을 가진다. (linearithmic complexity)
int i, j, k = 0;
for (i = n/2; i <= n; i++) {
for (j = 2; j <= n; j = j * 2) {
k = k + n/2;
}
}
5. O(n^2): 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱. (quadratic complexity)
function exampleQuadratic(n) {
for (let i = 0; i < n; i++) {
console.log(i);
for (let j = i; j < n; j++) {
console.log(j);
}
}
}==> 중첩 for문이 늘어나면 하나가 늘어날때 마다 n^2 ㅡㅡ> n^3 ㅡㅡ> n^4이렇게 늘어날 것이다.
6. O(C^n): 문제를 해결하기 위한 단계의 수는 주어진 상수값 C의 n 제곱. (exponential complexity)
function a(n){
if(n <= 0) {
return 0;
} else if(n === 1) {
return 1;
}
return a(n-1) + a(n-2);
}# 1초에 2천만번 연산하는 것을 생각했을 때 대략적인 시간을 예측할 수 있다. 이런 부분을 고려해서 코드를 작성할 경우 효율적인 코드를 도출할 수 있지 않을까 생각된다.
'다양한 Dev. > 기본 정리' 카테고리의 다른 글
| 2023.05.15 GitHub - Fork (0) | 2023.05.15 |
|---|---|
| 2023.05.11 - SQL vs noSQL (0) | 2023.05.11 |
| 2023.05.02 - 정규표현식(Regular Expression) (0) | 2023.05.02 |
| 2023.04.13 - HTTP란? (0) | 2023.04.13 |
| 2023.03.28 - GitHub 사용 방법 (0) | 2023.04.01 |
